散布図
散布図は、2種類のデータの関係を表すグラフの一種で、それぞれの項目を縦軸と横軸にとり、各データを該当する位置(縦軸と横軸の交わるところ)にプロット(打点)することで作成される図です。
散布図は、棒グラフや折れ線グラフと違って、作る機会は決して多くはありませんが、データの相関関係などを分かりやすく説明するためには、とても便利なグラフです。
ここでは、都道府県別の人口と県内総生産(GDP)を例にとって解説します。
散布図の作り方

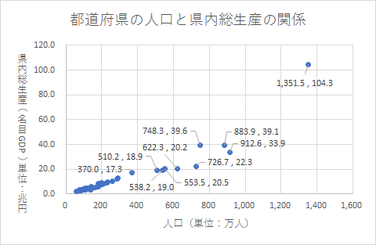
平成27年度県別人口と県内総生産(名目)
県内総生産の大きい順に並べたもの
出典:内閣府統計表
Excelで散布図を作成する時は、グラフ化するデータ 2 列を見出しを含めないで範囲選択します。
【便利知識】
左側の列が横軸(X軸)、右側の列が縦軸(Y軸)の値になります。
散布図ができあがってから縦軸と横軸を入れ替えることもできなくはありませんが、通常の操作ではなく面倒ですので、縦軸と横軸を入れ替える場合は、表を列を入れ替えてからグラフを作成し直した方が簡便です。
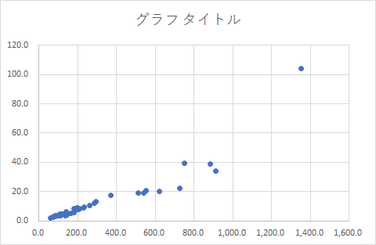
「挿入」タブをクリックし、「グラフの挿入」ダイアログボックスで、「散布図」の「散布図」で右側のグラフ(縦横の交差する箇所をプロットしている方)を選びます。

散布図へのデータラベル挿入
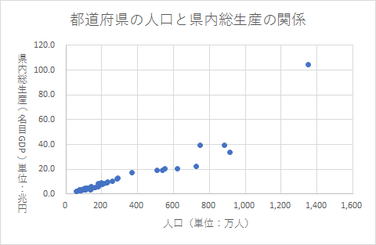
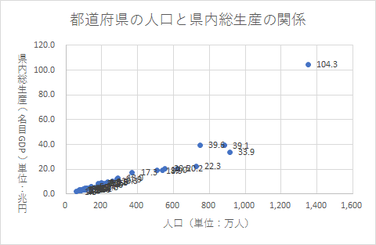
散布図にデータラベルを挿入すると、初期値では、縦軸(Y軸。このケースでは、県内総生産)の値のみが表示されます。
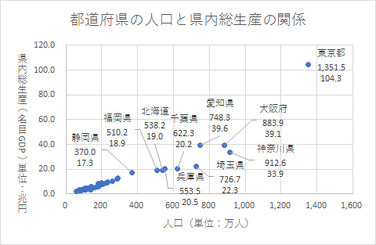
データラベルの「ラベルオプション」の設定で、横軸の値(X軸。このケースでは、人口)の値も表示できます。
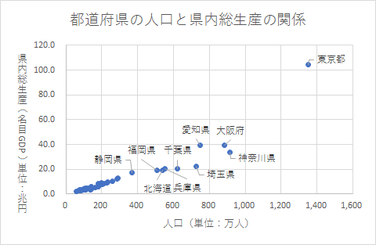
また、「セルの値」を選び、ラベル名となるセル範囲を指定することで、名称(このケースでは都道府県名)を表示させることもできます。
【便利知識】
プロットが密集している箇所のデータのデータラベルを表示しても見にくくなるだけで、あまり意味がありません。データラベルの表示は、「特異」なデータだけを選んで行うことをお勧めします。
【便利知識】
ラベルオプションの「セルの値」は、全てのデータを選択している状態でなければ表示されません。特定のデータのみのデータラベルで、名称(このケースでは都道府県名)を付けたい時は、データラベルを選んでおいて、数式バーに「=」を入力した後、都道府県名のセルを選びます。
【便利知識】
ラベルオプションの「セルの値」で名称(このケースでは都道府県名)のセル範囲を指定した場合には、同時に横軸(X軸。このケースでは人口)の値や縦軸(Y軸。このケースでは県内総生産)の値も表示させることができます。
特定のデータに対して、数列バーを使って名称を付けた時は、データラベルとして横軸、縦軸の値を表示させることはできません。
回帰直線
散布図において、プロットが右上がりであれば「正の相関」があり、右下がりであれば「負の相関」があると呼びます。また、どちらでもない場合は「無相関」であるといいます。
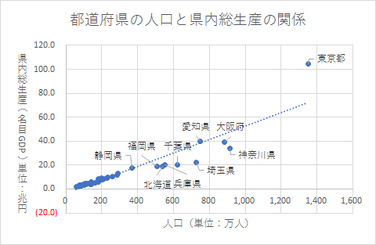
散布図に回帰直線などの近似曲線を描くと、相関関係が分かりやすくなります。
回帰直線とは、変化の割合がほぼ同じという場合の近似に用いられるもので、2組のデータの中心的な分布傾向を表す直線のことです。散布図に回帰直線を描いて将来的な値の予測に利用されることもあります。
詳しい説明は省きますが、回帰直線は、y=ax+b (a:傾き、b:切片(Y軸との交点の高さ))という一次方程式で示される直線で、aとbの値は最小二乗法という回帰分析の手法で求められるものです。
Excelでは回帰直線などの近似曲線を簡単に描くことができます。
散布図、棒グラフ、折れ線グラフなどのグラフを選択しておいて、「グラフ要素の追加」から「近似曲線」を選び、「線形」をクリックすれば、回帰直線が点線で描かれます。
近似曲線の種類と使い分け
Excelで描ける近似曲線には、線形近似(=回帰直線)、指数近似、累乗近似、対数近似、多項式近似と、移動平均の6つの種類があります。多項式近似では、2次から6次までの次数を選べます。
細かな説明は省きますが、以下の考え方で使い分けると良いでしょう。
データが右に行くほど増える(あるいは減る)時
変化の割合がほぼ同じ 線形 変化の割合がほぼ一定の時
変化の割合が大きくなっていく 指数 変化の割合が徐々に大きくなる時
あるいは累乗 変化の割合が特定の割合で加速度的に大きくなる時
変化の割合が小さくなっていく 対数 変化の割合が急激に減ってから横ばいになる場合
あるいは累乗 変化の割合が特定の割合で加速度的に小さくなる時
データが増えたり減ったりして波がある時 多項式
波が1つ(増えて減る、あるいは減って増える) 2次
波が2つ(増えて減って増える、あるいは減って増えて減る) 3次
波が3つ 4次
時系列データの長期的な傾向を見たい時 移動平均
近似曲線の数式と決定係数の表示
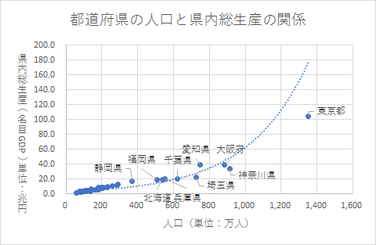
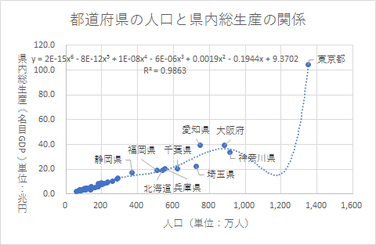
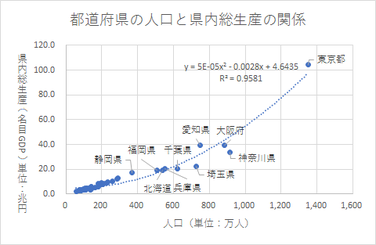
近似曲線の書式設定には、グラフ上に近似曲線の数式と、決定係数(R-2乗値=R2)を表示するオプションがあります。
決定係数は回帰分析モデルの当てはまり具合を示す指標のひとつで、1に近い値のものほど当てはまっていると言えます。
今回のケースでは、6次多項式近似曲線の決定係数が他の近似曲線よりも高い決定係数値を示しましたが、6次の数式にした理論的な根拠はなく、人口が1,000万人を超えたあたりの曲線が不自然です。今回のケースでは2次多項式近似曲線あたりが妥当と思われます。